Priority Queues
Priority Queue ADT
맵 ADT의 종류로써 키-값 아이템 컬렉션을 저장하고, 가장 작은 키만 삭제할 수 있다.
- insert(k, v): k의 키와 v의 값을 가지는 아이템을 넣는다.
- remove_min(): 가장 작은 키를 가진 아이템을 삭제하고 리턴한다.
- min(): 가장 작은 키를 가진 아이템을 리턴한다.
- size(): 보관된 아이템의 개수를 리턴한다.
- is_empty(): 큐가 비어있는지 확인한다.
min 대신에 max 버전도 있지만 동시에 사용할 수는 없다.
응용 예시: 모던 주식 거래 시스템은 matching engine으로 알려지는 시스템을 핵심으로 한다. 이 엔진은 구매자와 판매자의 주식 거래를 매칭시켜준다. 구매자는 특정 주식을 사기 위한 가격 제시를 할때 특정한 가격에, 혹은 그 이하를 제시한다. 판매자는 특정 주식을 특정 가격에 팔기 위한 제시를 한다. 이 때, 구매 오더와 판매 오더는 각각 priority queue에 저장되고 가격이 가장 높은 우선순위를 갖게 된다. 매칭 엔진은 새로운 오더가 들어올 때 마다 거래가 바로 성사될 수 있는지 확인하고, 그렇다면 거래를 하고 아니면 오더를 큐에 넣어준다.
Sequence-based Priority Queue
정렬되지 않은 리스트, 혹은 정렬된 리스트로 priority queue를 구현할 수 있다. 정렬되지 않은 리스트는 insert: O(1), remove_min/min: O(n) 시간 복잡도를 가지는 반면, 정렬된 리스트는 insert: O(n), remove_min/min: O(1) 시간 복잡도를 가진다. 둘 다 size/is_empty는 O(1)을 가진다.
우리는 priority queue를 써서 키 리스트를 정렬할 수 있다.
- 빈 priority queue에 키를 반복적으로 넣어준다.
- 반복적으로 remove_min을 하여 정렬한다.
위 슈도코드를 sequence-based priority queue로 구현하면 두 가지 경우 다 O(n^2) 시간 복잡도를 가진다.
Selection Sort (선택정렬)
정렬되지 않은 리스트 구현의 변형으로 볼 수 있다.
- n번의 insert 연산은 O(n)을 가진다.
- n번의 remove_min 연산은 O(n^2)을 가진다.
이때, 우리는 top level loop의 invariant는 다음과 같다고 말할 수 있다:
- A[0, i)는 정렬되있다.
- A[i, n)은 priority queue이고 모든 원소가 A[i-1]보다 크거나 같다.
예시:
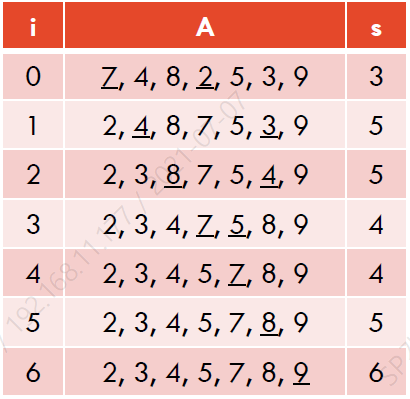
Insertion Sort (삽입정렬)
정렬된 리스트 구형의 변형으로 볼 수 있다.
- n번의 insert 연산은 O(n^2)을 가진다.
- n번의 remove_min 연산은 O(n)을 가진다.
이때, 우리는 top level loop의 invariant는 다음과 같다고 말할 수 있다:
- A(0, i]가 priority queue가 된다 - 따라서 정렬된다.
- A[i,n)는 삽입될 리스트이다.
예시:
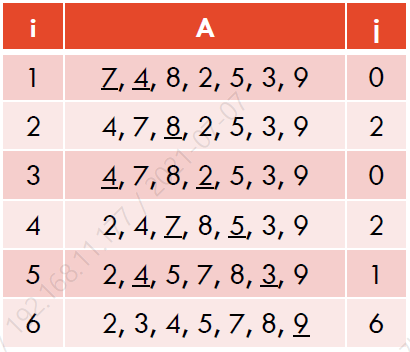
Heap Data Structure (min-heap)
자료구조 중 heap은 여러개의 노드로 구성된 이진 트리이다. 각 노드에는 (key, value) 아이템을 보관하고 다음과 같은 속성을 만족한다.
-
Heap-Order: 모든 노드 m != root 에 대해서 key(m) >= key(parent(m))
-
Complete Binary Tree: h가 트리의 높이일 때, 모든 레벨 i < h는 full하고 (i.e. 2^i개의 노드가 존재함), 나머지 노드들은 레벨 h의 leftmost 포지션을 가진다.
- Minimum of a heap Claim: root 노드는 항상 heap에서 가장 작은 키값을 가진다.
Proof: 최소 키값이 어떠한 노드 x에 있다고 가정하자. Heap 속성에 의해 트리의 위로 갈수록 키값은 작아질 수 밖에 없다. 만약 x가 root가 아니라면, 그것의 부모 노드 또한 최소 키값을 가지고 있어야 한다. root에 도달할 때 까지 반복한다.
- Height of a heap Claim: n개의 키를 가진 heap은 높이 log(n)을 가진다.
Proof: n개의 키를 가진 heap의 높이를 h라고 하자. depth i = 0, …, h - 1의 깊이에 각각 2^i개의 키가 있고, h에는 적어도 1개의 키가 있기 때문에 n >= 1 + 2 + 4 + … + 2^(h + 1) + 1이 성립된다. 따라서 n >= 2^h가 되고 양변에 로그를 취하면, log(n) >= h가 된다.
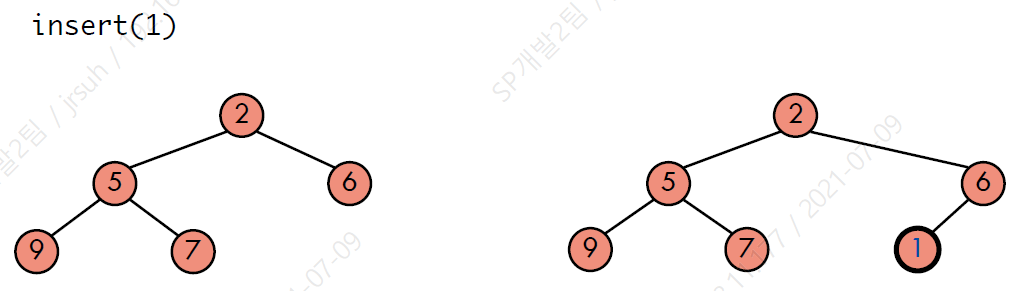
- Insertion into a heap
- 주어진 키를 가진 새로운 노드를 만든다.
- 새로운 노드를 삽입할 위치를 찾는다.
- heap-order 속성을 유지시킨다.
이때, heap-order 속성을 유지시키기 위해 upheap(heapify, bottom-up approach) 과정을 거친다. 이 과정은 삽입 포인트에서부터 위쪽으로 키를 바꾸는 것이다.
Pseudo code는 다음과 같다.
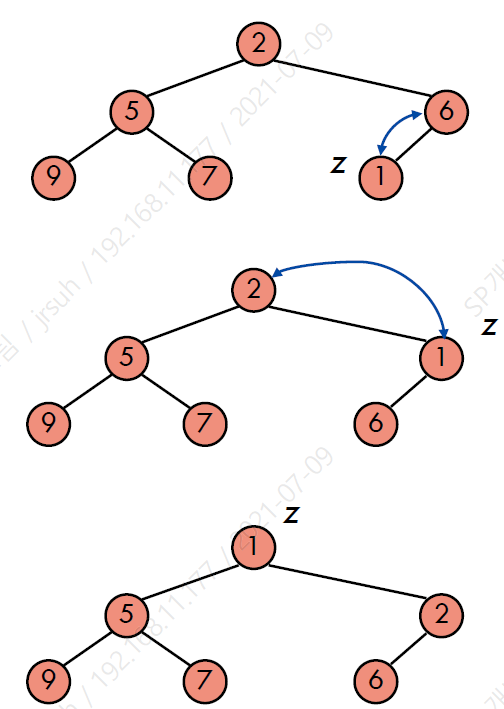
heap의 높이가 log n이기 때문에 시간 복잡도는 O(log n)이다.
heap에 새로운 노드를 삽입하기 위해 그 position을 찾아야할 경우도 있다. 그럴때, 다음과 같은 과정을 거치면 해당 position에 도착할 수 있다.
- 마지막 노드에서 시작한다.
- 왼쪽 자식 노드, 혹은 root 노드에 도착할 때 까지 위로 간다.
- 왼쪽 자식 노드에 도착했다면, 부모 노드의 오른쪽 자식 노드로 이동한다. 만약 root에 도착했다면 바로 4번을 수행한다 (새로운 레벨을 시작해야 함).
- leaf 노드에 도착할 때 까지 왼쪽 아래로 이동한다.
이 position 탐색 또한 O(log n)의 시간 복잡도를 가지므로 insertion 알고리즘의 전체 시간 복잡도는 O(log n)이 된다.
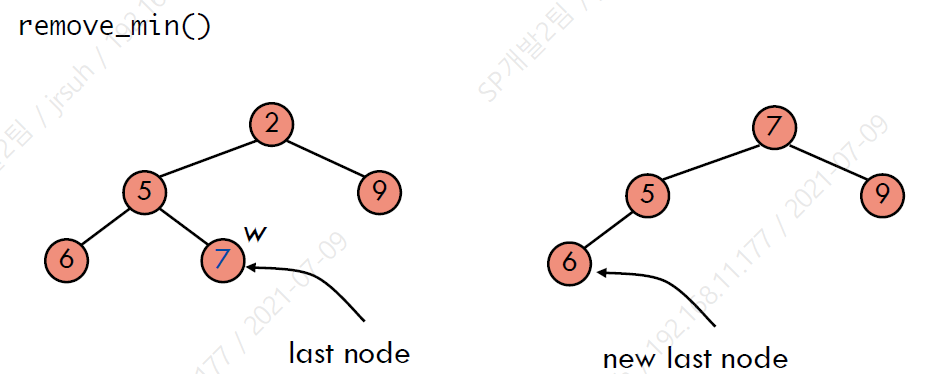
- Removal from a heap (remove_min)
- root 키를 마지막 노드 w의 키와 바꾼다.
- w를 삭제한다.
- heap-order 속성을 유지시킨다.
NOTE: root 노드가 최소 키값을 가지기 때문에, 이를 삭제하는 것이 목표이다.
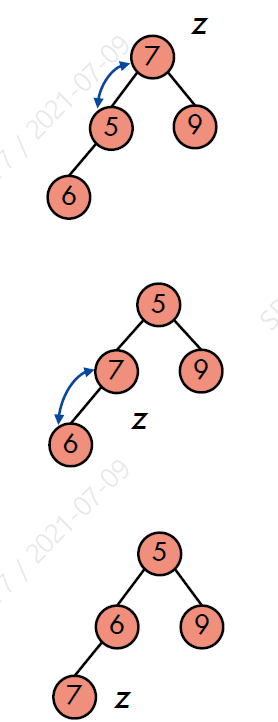
Insert와 마찬가지로 노드 삭제 후, heap-order 속성을 유지시키기 위해 downheap (heapify, top-down approach)를 수행한다.
heap의 높이가 log n이기 때문에 시간 복잡도는 O(log n)이다.
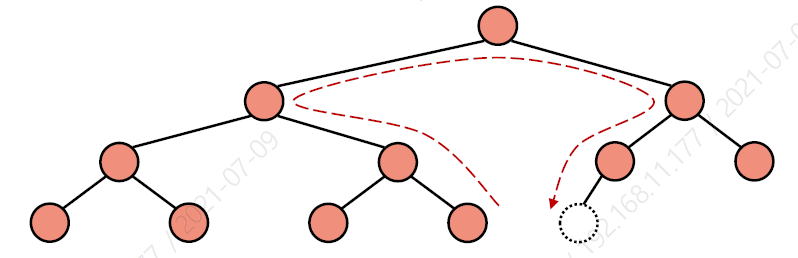
heap에서 노드를 삭제한 후, 새로운 마지막 노드를 탐색하기 위해 다음과 같은 과정을 거칠 수 있다.
- 이전 마지막 노드에서 시작한다.
- 오른쪽 자식 노드, 혹은 root 노드에 도착할 때 까지 위로 이동한다.
- 만약 오른쪽 자식 노드에 도착했다면, 부모 노드의 왼쪽 자식 노드로 이동한다. 만약 root 노드에 도착했다면, 4번을 수행한다 (레벨을 닫아야 함).
- leaf 노드에 도착할 때 까지 오른쪽 아래로 이동한다.
새로운 마지막 노드 위치 탐색의 경우도 O(log n)이 걸리므로 (트리의 높이가 log n이기 때문에), remove의 전체 시간 복잡도는 O(log n)이다.
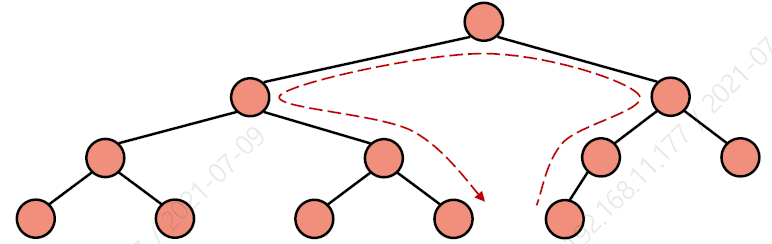
이와 같이 heap 구조를 기반으로 한 priority queue를 구현할 수도 있는 것이다.
Heap Sort
heap으로 구현된 n개의 아이템을 갖는 priority queue를 생각해보자. 사용된 공간은 O(n)이고, insert와 remove_min 메소드는 각각 O(log n)의 시간이 걸린다. Priority queue를 정렬하기 위해 n번의 insert 연산과 n번의 remove_min 연산이 필요하다는 것을 기억하자.
Heap sort는 heap으로 구현된 priority queue 정렬의 한 버전으로써 O(nlog n)의 시간 복잡도를 가진다.
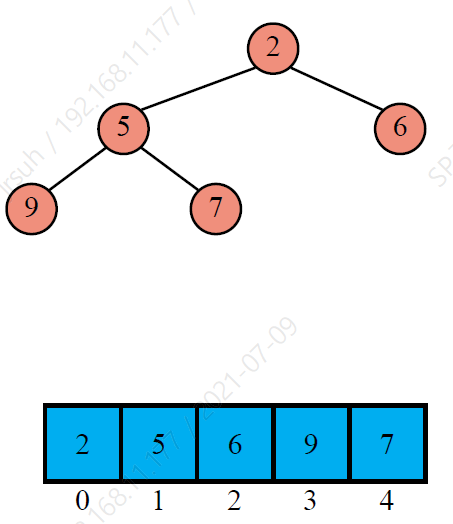
Heap-in-array 구현
n개의 키를 갖는 heap을 길이 n의 배열로 나타낼 수 있다.
특수 노드: root는 0에 있고 마지막 노드는 n - 1에 있다.
인덱스 i에 있는 노드:
- 왼쪽 자식 노드는 2i + 1에 있다.
- 오른쪽 자식 노드는 2i + 2에 있다.
- 부모 노드는 floor[(i - 1) / 2]에 있다.
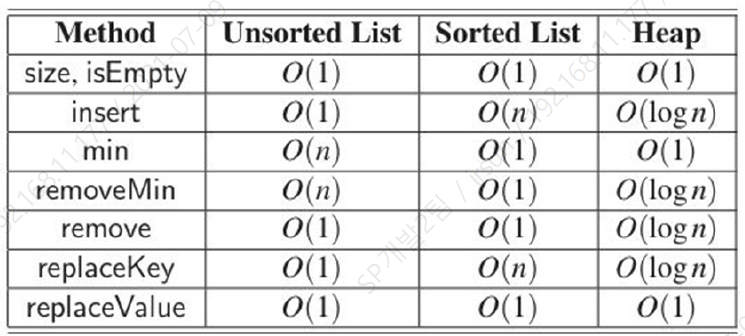
Priority Queue 구현체들의 메소드 시간 복잡도를 비교하면 다음과 같다.
Leave a comment