Secure Hash Algorithm

개요

Secure Hash Algorithm (SHA)는 National Institutes of Standards and Technology (NIST)와 정부 및 개인 연구 그룹에서 개발한 데이터를 보호하기 위한 암호화 알고리즘의 집합이다. 이 알고리즘들은 해시 함수(Hash Function)를 사용하여 데이터를 변환시킨다.

이러한 해시 함수는 여러 과정을 통해 원래의 데이터를 전혀 다른 형태의 문자열로 변환해준다. SHA-1, SHA-2, SHA-3는 각각 점차적으로 강력해지는 암호화를 통해 설계된 알고리즘이다. SHA-0은 현재는 너무나 많은 취약점이 노출되어 퇴화된(obsolete) 상태이다.

SHA의 가장 흔한 응용은 비밀번호를 암호화하는 것이다 - 서버에서 특정 유저의 실제 비밀번호를 저장하지 않고, 해시 값만 저장하면 되기 때문이다. 이를 통해 해커가 데이터베이스를 공격하여도, 해시로 암호화된 문자열만 볼 수 있을 것이다. 또한, SHA는 눈사태 효과(avalanche effect) 속성을 갖는다 - 암호화될 데이터가 조금만 바뀌어도 아웃풋이 크게 바뀌는 것, 혹은 반대로 기존 데이터의 큰 변화는 비슷한 해시 값을 불러오는 것을 말한다. 이러한 속성은 해시 값이 인풋 스트링에 대한 정보를 노출하지 않도록 해준다. 그리고 이러한 효과를 사용하여 공격자가 데이터를 변경했는지도 쉽게 알 수 있다.

SHA 특징

암호화 해시 함수는 세 가지 근본적인 안전성 특징을 통해 데이터 보안을 책임진다:

1. pre-image resistance
2. second pre-image resistance
3. collision resistance

암호화 기법의 초석은 pre-image resistance를 제공하는 것이다. 이는 다시 말해 공격자가 해시 값 $h_{m}$을 알고 있을 때, 원래의 메시지 $m$을 찾는 것을 매우 어렵게, 혹은 시간이 오래 걸리게 하는 것을 말한다. 이는 one-way function의 특성에 의해 제공되는데, SHA의 핵심 요소라고 볼 수 있다. Pre-image resistance를 통해 강력한 컴퓨팅 파워를 통한 브루트포스 공격을 막을 수 있다.

One-way Function Example

Alice와 Bob은 우편을 통해 의견을 교환한다. Alice가 Bob을 방문했을 때, 그녀가 사는 도시의 전화번호부를 주었다. 외부자로부터 그들의 메시지를 노출하지 않기 위해 Alice는 Bob에게 메시지를 암호화하겠다고 말하였다. 그녀는 각 편지에 특정 조합의 숫자들이 있을 것이고 각 숫자 시퀀스는 전화번호를 나타낸다고 말한다. Bob은 그 전화번호를 전화번호부에서 찾아서 해당 사람의 성의 첫 문자를 적으면 된다. 이러한 ‘함수’를 통해 Bob은 전체 메시지를 복호화할 수 있다.

메시지를 복화하하기 위해, Bob은 전체 전화번호부를 읽어서 편지에 있는 모든 숫자들을 찾아야 하지만, Alice는 메시지를 암호화하기 위해 문자를 빠르게 찾아서 그에 해당하는 전화번호를 적기만 하면 된다. 이러한 이유 때문에, Bob이 메시지를 일일이 복화하기 전에, Alice는 메시지를 재암호화하여 데이터를 안전하게 유지할 수 있다. 따라서 Alice의 알고리즘은 one-way function이다. 즉, one-way function은 한 쪽으로 값을 구하는 것은 쉽고 빠르지만, 반대쪽의 값, 즉 inverse 값을 구하는 것은 매우 어렵다. 여기서 쉽고 어렵다의 기준은 계산의 복잡도의 맥락으로 이해할 수 있다.

두 번째 안전성 특징은 second pre-image resistance이다. 이는 하나의 메시지 $m_{1}$을 알고 있을 때, 동일한 해시 값 $H_{m_{1}} = H_{m_{2}}$로 매핑되는 또 다른 메시지 $m_{2}$를 찾기가 어려운 것이다. 이 특징이 없다면 두 개의 다른 비밀번호가 동일한 해시 값으로 매핑되어, 보호된 데이터에 접근하기 위해 원래의 비밀번호가 쓸모없어 지는 것을 의미한다.

마지막 안전성 특징은 collision resistance이다. 이는 공격자가 동일한 해시 값 $H_{m_{1}} = H_{m_{2}}$로 매핑되는 두 개의 완전히 다른 메시지를 찾는 것을 매우 어렵게 만드는 것이다. 이 특징을 제공하기 위해서는 비슷한 개수의 가능한 인풋과 가능한 아웃풋이 있어야 한다. 왜냐하면 인풋이 아웃풋 보다 많으면 비둘기집 원리에 의해 충돌이 무조건 발생하기 때문이다. 따라서 collision resistance가 있다면 동일한 해시 값으로 매핑되는 두 개의 인풋을 찾는 것이 매우 어려워진다. 이러한 특징이 없다면 디지털 서명에 이러한 점을 악용하여 한 사람이 동일한 해시 값으로 두 개의 문서를 서명하였는데, 유저들은 이것이 두 명의 다른 사람에 의해 작성된 두 개의 문서라고 믿을 수 있는 것이다.

일반적인 가이드라인으로 해시 함수는 최대한 랜덤해야하되, deterministic하고 계산이 빠르게 되어야 한다.

SHA-1

SHA-1은 1993년도에 NIST에 의해 개발되어 TLS, SSL, PGP, SSH, IPsec 및 S/MIME 등의 보안 어플리케이션 및 프로토콜에 광범위하게 사용되었다.

SHA-1은 메시지를 $2^{64}$ bits 이하의 길이의 bit string의 형태로 인풋을 주어 160-bit 해시 값을 제공하는데, 이러한 해시 값을 message digest라 부른다. 아래 예시에서는 간결함을 유지하기 위해 hexadecimal로 메시지를 표시하겠다.

SHA-1을 사용하여 메시지를 암호화하는 두가지 방법이 있다. 그중 한 가지 방법은 64개의 32-bit 단어를 처리해야하는 과정을 줄여주지만 실행하기 위해서는 더욱 복잡하고 시간이 걸린다. 아래 예시에서는 더 간단한 방법을 소개한다. 실행이 끝나면 알고리즘은 16개의 단어의 블록들을 아웃풋으로 내보내는데, 각 단어는 16 bits이므로 총 256 bits가 결과로 나온다.

Pseudocode

메시지 ‘abc’를 SHA-1로 인코딩한다고 가정해보자.

‘abc’는 바이너리 형태로 $01100001\;01100010\;01100011$이다.

Step 1. 첫 단계는 다섯 개의 랜덤한 hex 문자들로 구성된 스트링을 초기화하는 것이다. 각각은 해시 함수의 일부분이 될 것이다.

\[\begin{align*} H_{0} &= 67DE2A01 \\ H_{1} &= BB03E28C \\ H_{2} &= 011EF1DC \\ H_{3} &= 9293E9E2 \\ H_{4} &= CDEF23A9 \end{align*}\]

Step 2. 다음으로 메시지 끝에 1을 한개 붙여줌으로써 패딩을 해주고 메시지가 총 448 bits가 될 때 까지 0을 붙여준다. 그리고 메시지의 길이를 64 bits로 나타낸 것을 또 붙여줌으로써 512 bits의 메시지가 나오게 된다.

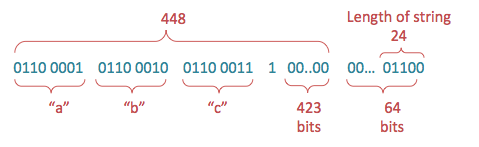
Step 3. 위에서 얻은 패딩된 인풋 $M$을 512-bit 블록으로 나누고 각 블록은 한번 더 16개의 32-bit 단어들 $W_{0}, \ldots, W_{15}$로 나눈다. ‘abc’의 경우, 메시지가 총 512 bits보다 적기 때문에 오로지 하나의 블록만 있다.

Step 4. 각 블록에 대해서 해싱을 위한 80번의 iteration을 시작한다 (80는 SHA-1에서 결정된 숫자이다). 각 iteration에서 각 블록에 대하여 특정 연산을 수행한다.

Iteration $16 \leq i \leq 79$ 까지는 다음의 연산을 수행한다.

\[W(i) = S^{1}(W(i - 3) \oplus W(i - 8) \oplus W(i - 14) \oplus W(i - 16))\]

여기서, $\oplus$ 는 XOR (exclusive OR) 논리 연산자이고, $W(i)$ 는 word라고 칭한다.

예를 들어, $i = 16$ 인 경우, $W(16)$ 는 다음과 같이 구해진다.

\[\begin{align*} W(16) &= S^{1}(W(13) \oplus W(8) \oplus W(2) \oplus W(0)) \\ &= \text{00000000 00000000 00000000 00000000} \\ &\oplus \text{ 00000000 00000000 00000000 00000000} \\ &\oplus \text{ 00000000 00000000 00000000 00000000} \\ &\oplus \text{ 01100001 01100010 01100011 10000000} \\ &= \text{ 01100001 01100010 01100011 10000000} \end{align*}\]

Step 5. Circular Shift Operation

Word $X$ 에 대한 $n$ bits의 Circular shift operation $S^{n}(X)$ 은 다음과 같의 정의한다.

\[S^{n}(X) = (X << n) \text{ OR } (X >> 32 -n)\]

여기서, $0 < n < 32$ 이고, $X « n$ 은 left-shift 연산: $X$ 의 leftmost $n$ bits를 버리고, 왼쪽으로 이동시킨 후, 오른쪽에 $n$ 개의 0을 채운다. 그리고, $X » 32 - n$ 은 right-shift 연산: $X$ 의 rightmost $n$ bits를 버리고, 오른쪽으로 이동시킨 후, 왼쪽에 $n$ 개의 0을 채운다. 따라서 $S^{n}X$는 $X$에 대한 $n$개의 포지션을 circular shift하는 것을 의미한다.

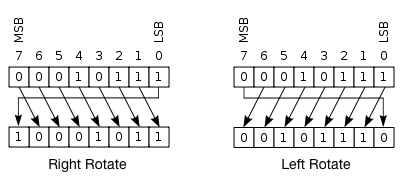
연산을 수행하면 $W(16)$은 $\text{ 11000010 11000100 11000111 000000000}$가 된다.

Step 6. Step 1에서 정의된 해시 값들을 다음 변수들에 저장한다.

\[A = H_{0} B = H_{1} C = H_{2} D = H_{3} E = H_{4}\]

Step 7. 80 iteration 동안($0 \leq i \leq 79$), 다음을 계산한다.

\[\text{TEMP} = S^5 * A + f(i; B, C, D) + E + W(i) + K(i)\]

TEMP를 구한 후, 다음과 같이 변수를 재할당한다.

이 때, $f(i; B, C, D)$는 세 개의 32-bit 단어인 $B$, $C$, $D$, 에 대해 $i$ 값에 따라 논리 연산을 수행하는 함수이고, 32-bit 아웃풋을 준다. 함수들은 다음과 같다.

\[\begin{align*} f(i; B, C, D) &= (B \land C) \lor ((\lnot B) \land D) &\qquad \text{ for } 0 \geq i \geq 19 \\ f(i; B, C, D) &= B \oplus C \oplus D &\qquad \text{ for } 20 \geq i \geq 39 \\ f(i; B, C, D) &= (B \land C) \lor (B \land D) \lor (C \land D) &\qquad \text{ for } 40 \geq i \geq 59 \\ f(i; B, C, D) &= B \oplus C \oplus D &\qquad \text{ for } 60 \geq i \geq 79 \end{align*}\]

또한, $K(i)$는 다음과 같이 hex constant로 정의된다.

\[\begin{align*} K(i) &= \text{5A827999} &\qquad \text{ for } 0 \geq i \geq 19 \\ K(i) &= \text{6ED9EBA1} &\qquad \text{ for } 20 \geq i \geq 39 \\ K(i) &= \text{8F1BBCDC} &\qquad \text{ for } 40 \geq i \geq 59 \\ K(i) &= \text{CA62C1D6} &\qquad \text{ for } 60 \geq i \geq 79 \end{align*}\] \[E = D D = C C = S^{30}(B) B = A A = \text{TEMP}\]

Step 8. 현 블록의 해시 값을 모든 블록들에 대한 전체 해시 값에 더한 후, 다음 블록을 처리한다.

\[H_{0} = H_{0} + A H_{1} = H_{1} + B H_{2} = H_{2} + C H_{3} = H_{3} + D H_{4} = H_{4} + E\]

Step 9. 모든 블록들이 처리되면 5개의 해시 값들을 OR 논리 연산자인 $\lor$로 연결한 160-bit 문자열로 나타낸 message digest를 만든다.

\[HH = S^{128}(H_{0}) \lor S^{96}(H_{1}) \lor S^{64}(H_{2}) \lor S^{32}(H_{3}) \lor H^{4}\]

결과적으로 문자열 ‘abc’는 a9993e364706816aba3e25717850c26c9cd0d89d의 해시 값을 갖게 된다.

만약 문자열이 약간 바뀌어 ‘abcd’가 되면, 해시 값은 81fe8bfe87576c3ecb22426f8e57847382917acf로 매우 다르게 바뀌어서 공격자들이 원래의 메시지와 비슷할 것이라 예측할 수 없다.

SHA-1은 아직 많이 쓰이고 있지만, 2005년에 암호 해독가들에 의해 알고리즘에 취약점이 발견되었다. 이 취약점은 여러 개의 다른 인풋을 사용하여 매우 빠르게 충돌(collision), 즉 두 개의 다른 인풋이 동일한 digest와 매핑되는 것을 찾는 알고리즘에 의해 발생하였다.

2010년 후에 여러 개의 기업들은 SHA-2나 SHA-3로 업그레이드하는 것을 권장하였다.

SHA-2

SHA-1의 취약점 발견으로 인해, 암호 해독가들은 알고리즘을 보완하여 SHA-2를 만들었다. SHA-2는 한 개의 해시 함수가 아니라 각각 32, 64-bit 단어들을 사용하는 SHA-256과 SHA-512, 두 개의 해시 함수로 구성되어 있다.

SHA-1은 160-bit 크기의 digest를 만들지만, SHA-2는 224나 256-bit 크기의 digest를 만든다는 점에서 크게 다르다. 또한, SHA-2에서는 블록 크기가 512 bits나 1024 bits가 될 수 있다.

SHA-2에 대한 브루트 포스 공격 또한 SHA-1을 대상으로 한 것 보다 효과적이지 않다. 길이가 $L$인 digest에 대응되는 메시지를 찾으려면 $2^{L}$만큼의 값을 구해야하므로 브루트 포스 공격에 대해서는 안전하다. 이 공격이 성공하는 시간은 메시지의 길이에 비례하기 때문에 SHA-1의 160-bit가 SHA-2에서 더 길어진 것이다.

결론

암호학이 이렇게 빨리 발전할 수 있었던 것은, 그만큼 많은 공격들이 이루어지고 있다는 뜻일 것이다. 가장 흔한 공격 중 하나가 역상 공격 (preimage attack)인데, 이는 미리 계산된 값 테이블을 갖고 브루트포스로 비교하여 패스워드를 크랙킹하는 것이다. 이 공격에 대한 해결법은 공격자가 주어진 해시 값에 대한 메시지를 찾기 위해 엄청난 양의 자원과 시간을 걸리게 하는 것이다. 이 외에도, 수학적 특성을 사용한 공격, 예를 들어 생일 공격 (birthday attack)이 있는데, 이 또한, 해시 충돌을 찾아내기 위해 생일 문제 (birthday problem)의 확률적 결과를 기반으로 한다. 생일 문제에 따르면 해시 함수의 입력값을 다양하게 할수록 해시 값이 같은 두 입력값을 발견할 확률이 빠르게 증가한다. 즉, 모든 값을 대입하지 않고도 해시 충돌을 찾을 수 있는 확률을 크게 높일 수 있다는 사실을 활용한다.

출처

https://brilliant.org/wiki/secure-hashing-algorithms/